

There are five important values to remember if you want to divide your data into quartiles. The quartiles separate the data into four equally sized parts. When we are working with a larger set of data it is much easier to separate the data into quartiles. The bigger the range the bigger is the measure of variation.
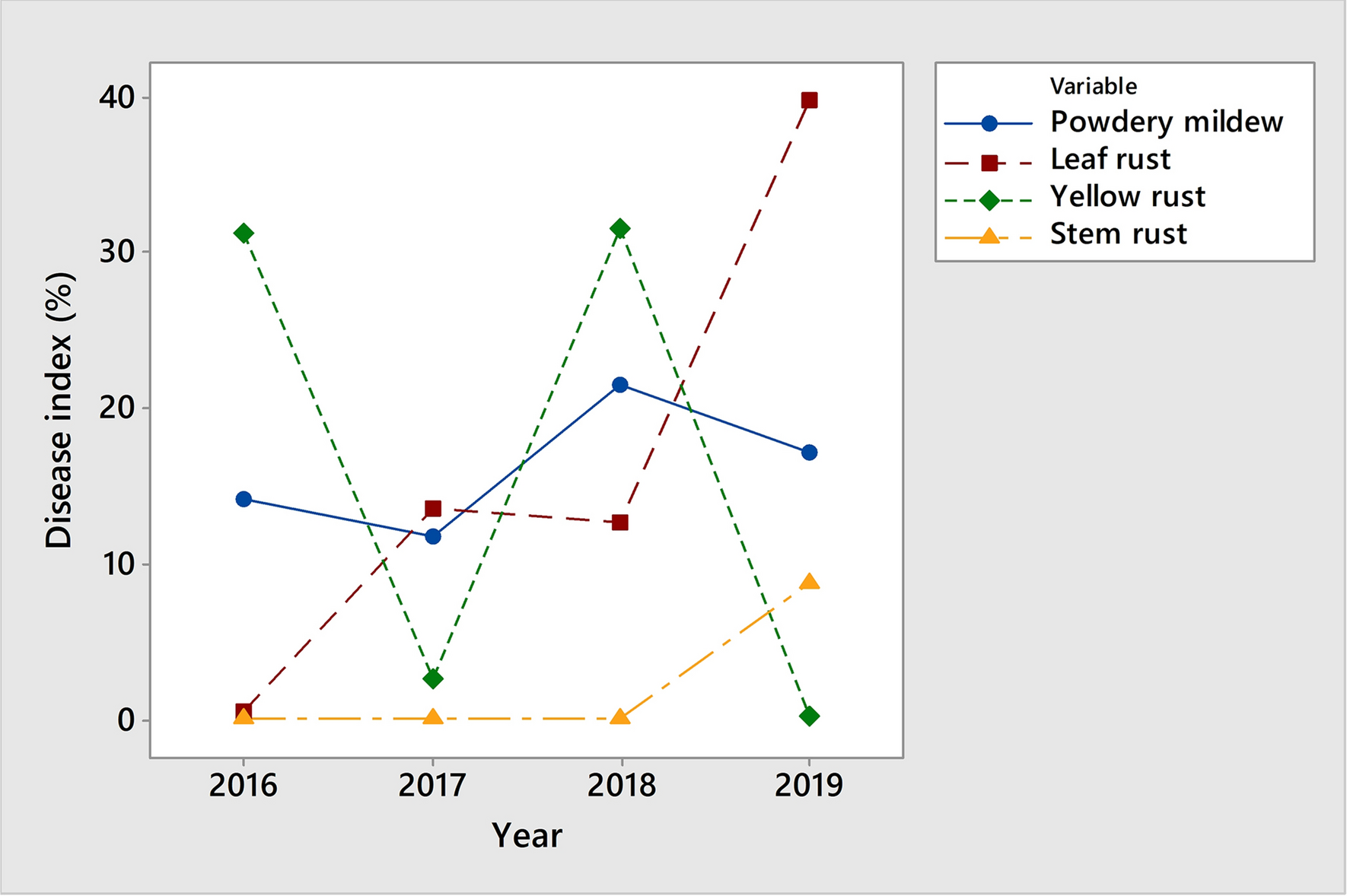
When we calculate the measure of variation we first calculate the difference between the greatest and the lowest values.
USING MINITAB EXPRESS TO DO A STEM AND LEAF PLOT SERIES
if we have the two number series A (10, 23, 50, 72, 90) and B (48, 49, 50, 51, 52) we can see that they both have the same median, but that there is a huge difference in variation. We then need to use the measure of variation e.g. We have already learned about the median, the mode and the mean but sometimes these don't fully describe a set of data. On the left hand side of the line we write the numbers that corresponds to the tens, 12 has 1 in the tens place and 33 has 3 in the tens place.
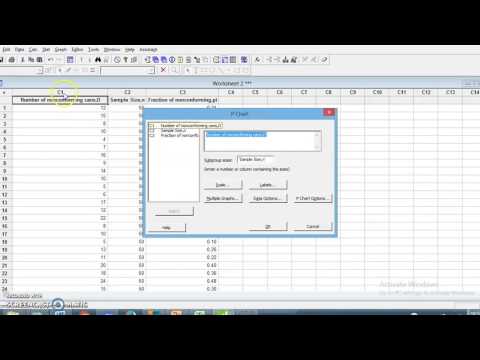
We begin by finding the lowest and the greatest number in the data set. This could for instance be the results from a math test taken by a group of students at the Mathplanet School.ġ3, 24, 22, 15, 33, 32, 12, 31, 26, 28, 14, 19, 20, 22, 31, 15 To set up a stem-and-leaf plot we follow some simple steps.įirst we have a set of data. A stem-and-leaf plot is used to visualize data. Stat > Nonparametrics > Mann-Whitney Confidence intervals and hypothesis tests for paired data Stat > Basic Stats > Paired tįorm differences (post-pre, before-after, second-first, etc.) and then use the one sample procedures on the differences.One way to measure and display data is to use a stem-and-leaf plot. Stat > Basic Statistics > 2-Sample t Confidence intervals and hypothesis tests for two medians Stat > Basic Statistics > 1-Sample t Confidence intervals and hypothesis tests for one median Stat > Nonparametrics > 1-Sample Sign Confidence intervals and hypothesis tests for two means Stat > Basic Statistics > 1 Sample Z (not realistic) Stat > Basic Statistics > 2 Proportions Confidence intervals and hypothesis tests for one mean Stat > Basic Statistics > 1 Proportion Confidence intervals and hypothesis tests for two proportions Stat > Regression > Fitted Line Plot Generating Random Numbers - Calc > Random Data Any Probability Distribution - Graph > Probability Distribution Plot Binomial Distributions - Calc > Probability Distributions > BinomialĬumulative Probability - P(X Probability Distributions Geometric Poisson Distributions - Calc > Probability Distributions Poisson Negative Binomial Distributions - Calc > Probability Distributions Negative Binomial Confidence intervals and hypothesis tests for one proportion Residual plots - Stat > Regression > Regression > Graphs Nonlinear Relationships
Scatterplot with regression line - Stat > Regression > Fitted Line Plot Prediction and assessing the fitįitted values and residuals - Stat > Regression > Regression > Storage > Fits and Residuals Time plots - Graph > Scatterplot OR Graph > Time series plot Measuring the strength of association Pearson's Correlation - Stat > Basic Statistics > Correlation Fitting a line to data Least squares regression line - Stat > Regression > Regression Scatterplot Smoothing - Graph > Scatterplot > Data View > Smoother > LOWESS Stat > Basic Statistics > Display Descriptive StatisticsĬreating New Variables - Calc > Calculator Standardizing a variable: z-ScoresĬalc > Standardize Association and relationship between 2 quantitative variables Mean, trimmed mean, median, standard deviation, quartiles, 5 number summary Minitab Commands Summary of Minitab Commands Graphical Displays Bar Graphs - Graph > Chartīoxplots - Graph > Boxplot Describing and Summarizing Data


 0 kommentar(er)
0 kommentar(er)
